Webb tanssii taivaalla Lagrangen ja Lissajousin kanssa
James Webb -avaruusteleskooppi saapui eilen maanantaina asemapaikalleen Lagrangen pisteessä 2. Olen itsekin kertonut näin teleskoopista tekemissäni jutuissa, vaikka oikeasti lause on vähän väärin: Webb, kuten muut L2:ssa ”olevat” avaruuslaitteet, kiertävät pistettä väkipakolla. Ellei niitä paimennettaisi, ne karkaisisivat omille teilleen planeettainvälisessä avaruudessa.

Terveisiä kiertoradalta herää taas horroksestaan ja menee hieman erikoisemmalle kiertoradalle, Lagrangen piste 2:n ympärillä olevalle sellaiselle.
L2 on ollut minulle kovin läheinen asia pitkän aikaa, sillä pääsin seuraamaan toimittajahattu päässäni varsin läheisesti paitsi nyt James Webb -teleskoopin tekemistä ja laukaisemista, niin myös sitä edeltäneiden L2:een lähetettyjen Planck, Herschel ja Gaia -alusten tekemistä.
Tähtitieteilijälle Lagrangen piste 2 onkin rakas, sillä se sopii erinomaisesti juuri taivaan tarkkailuun. Se on noin 1,5 miljoonan kilometrin päässä maapallosta, meistä ”ulospäin” aurinkokunnassa katsottuna. Maa, Aurinko ja Kuu ovat sieltä katsottuna samalla suunnalla, ja siksi havaintoja voidaan tehdä koko ajan katsomalla niistä poispäin. Noin 40 % taivaasta on koko ajan havaittavissa, kun otetaan huomioon varoalueet Auringon suunnalla (herkillä havaintolaitteilla ei kannata vilkaistakaan Auringon suuntaan), ja vuoden kuluessa L2:ssa oleva teleskooppi pystyy skannaamaan hyvin koko tähtitaivaan.
Eurooppalaisen tähtitaivaan kartoittajan Gaian lisäksi L2-pisteessä on tällä haavaa lisäksi venäläis-saksalainen röntgenteleskooppi Spektr-RG. Ja nyt siis myös James Webb -teleskooppi.

Mikä on Lagrangen piste?
Taustalla on kuuluisa kolmen kappaleen ongelma, eli kysymys siitä, miten kolmen kappaleen liikeradat lasketaan, kun ja jos näiden kappaleiden massat, sijainnit ja nopeudet tunnetaan jonain tiettynä hetkenä.
Painovoimalait muotoillut Isaac Newton pohti tätä kinkkistä asiaa jo vuonna 1687 kuuluisassa Principia-kirjassaan, mutta Leonhard Euler sai niistä esiin jo jotain konkreettista noin 80 vuotta myöhemmin. Hän löysi kolme tasapainopistettä, missä oleva pienimassainen kappale pysyisi jotakuinkin paikallaan ollessaan kahden suuren kappaleen läheisyydessä.
Pisteitä ei kuitenkaan kutsuta Eulerin pisteiksi vaan Lagrangen pisteiksi siitä syystä, että Joseph-Louis Lagrange julkaisi vuonna 1772 kirjoituksen nimeltä ”Essee kolmen kappaleen probleemasta”, ja siinä hän määritteli kaikkiaan viisi pistettä, missä vetovoimat jotakuinkin kumoavat toisensa kolmen kappaleen järjestelmässä.
Kyse on siis siitä, että kaksi suurehkoa ja massiivista kappaletta muodostavat ympärilleen painovoimakentän, missä on viisi aluetta, joihin kolmas, selvästi pienempi kappale jää vähän kuin jumiin; kappaleet vetävät sitä puoleensa samalla voimalla, joten se ei ala putoamaan kohti jompaa kumpaa kappaletta, vaan on vähän kuin nalkissa.
Tarkalleen ottaen Lagrangen pisteissä kahden toisiaan kiertävän massapisteen vetovoimat sekä keskipakoisvoima kumoavat toisensa niin, että edellisiin verrattuna selvästi pienempi kolmas massa voi pysytellä niissä paikoillaan suhteessa kahteen isompaan kappaleeseen.
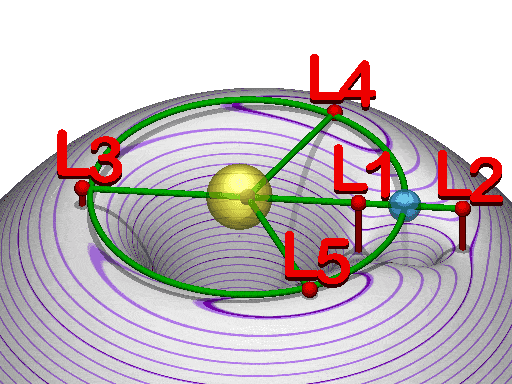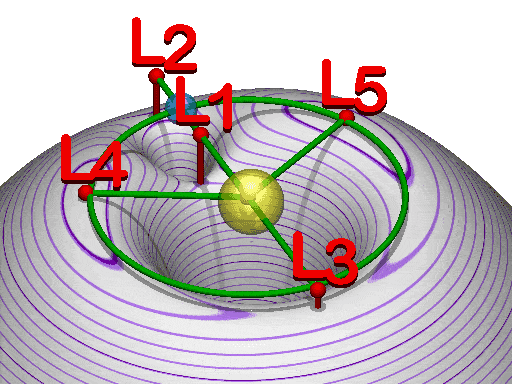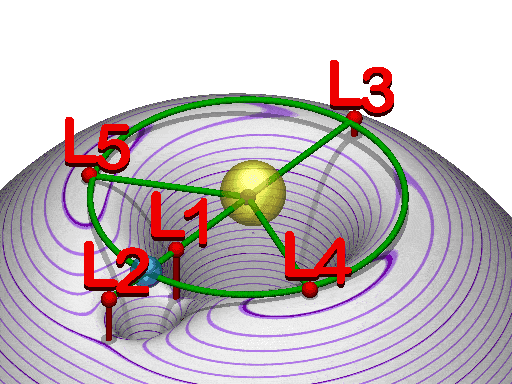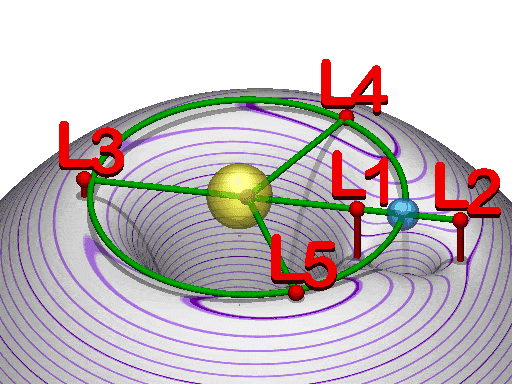
Maan ja Auringon tapauksessa piste 1, Lagrangen piste 1 eli L1, sijaitsee 1,5 miljoonaa kilometriä Maasta Auringon suuntaan ja L2 on saman verran meistä poispäin. L3 on puolestaan Maan etäisyydellä Auringosta täsmälleen vastakkaisella puolella Aurinkoa Maasta katsottuna.
L4 ja L5 ovat Maan radalla meistä katsottuna 60° kulmassa Auringosta katsottuna Maan vieressä. Ne siis kiertävät Aurinkoa samaan tapaan kuin Maa.
Jos L2 on omiaan tähtitieteellisille havainnoille, sopii L1-piste, joka on 1,5 miljoonan kilometrin päässä Maasta Auringon suuntaan, hyvin Aurinkoa tarkkaileville laitteille. Siellä on esimerkiksi SOHO-aurinko-observatorio.
L3 sijaitsee puolestaan täsmälleen Auringon toisella puolella, joten siellä olevaan laitteeseen ei voi olla suoraan yhteydessä. Sen sijaan jos olisi vieras sivilisaatio, joka koittaa hivuttautua Aurinkokuntaamme ihmiskunnan huomaamatta, niin veisin avaruusalukseni juuri Maan L3-pisteeseen.
L4- ja L5-sopisivat hyvin myös Aurinkoa tarkkaileville avaruusaluksille. Jos tässäkin mennään hieman tieteistarinoiden puolelle, niin nämä pisteet olisivat myös erinomaisia paikkoja avaruusasemille, sillä ne olisivat varsin lähellä Maata ja niistä olisi kätevää lähteä myös matkaamaan ympäri Aurinkokuntaa.
Lissajous ja hänen jännä ratansa
Siinä missä pisteisiin 4 ja 5 laitetut avaruuslaitteet pysyvät paikoillaan varsin hyvin, pyrkivät pisteissä 1, 2 ja 3 olevat laitteet karkaamaan pois. Käytännössä ne ajautuisivat vähitellen omille teilleen, ellei niitä pidettäisi pienin ratamuutoksin paikoillaan.
Ja paikallaan oleminen tarkoittaa tässä jännää rataa pisteen ympärillä. Fyysikko Jules Antoine Lissajous kehitti 1800-luvun puolivälissä soikiomaisesti epäkeskoja rinkuloita ja sellainen on myös hänen nimeään kantava rata, jollaisella Lagrangen pisteen ymärillä avaruuslaitteet kiertävät.
Niin sanotulla haloradalla Lagrangeen pisteen ympärillä oleva avaruusalus tarvitsee vain silloin tällöin pieniä ratakorjauksia, eli se pystyy olemaan tällaisella radalla hyvin pitkän aikaa.
Niinpä L1- ja L2-pisteissä ”olevat” avaruusalukset tekevät koko ajan pientä rinkulaa tyhjässä avaruudessa olevan matemaattisen pisteen ympärillä. Ja jotta näillä seuduilla ei tulisi tungosta, pyritään avaruusalukset vempauttamaan pois Lissajousin radalta Aurinkoa kiertämään toiminta-aikansa päätteeksi viimeisillä polttoainepisaroilla.
Näin tehtiin esimerkiksi Herschel- ja Planck-observatorioille, ja niin tehdään aikanaan myös Webbille.
Esimerkiksi Herschel kiertää nyt Aurinkoa radalla, joka on hieman maapalloa kauempana Auringosta. Se tulee tällä radallaan noin 300 vuoden kulutta uudelleen maapallon läheisyyteen, mutta pysyttelee silloinkin turvallisen välimatkan päässä – siitä ei ole meille tai muille avaruuslaitteille haittaa.
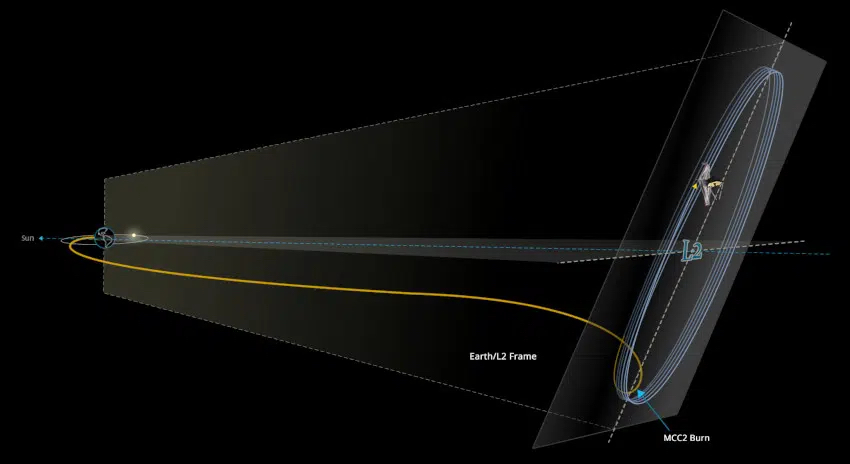
Miten Lagrangen pisteeseen mennään?
Otetaan esimerkiksi Webb. Kun se laukaistiin matkaan joulupäivänä 2021, sysäsi Ariane 5 -kantoraketti sen suoraan siirtoradalle kohti Lagrangen pistettä. Eli Arianen ylin vaihe sompasi reittiään siten, että Webb irtosi maapallon painovoimaikeestä ja siirtyi sellaiselle Aurinkoa kiertävälle radalle, millä Webb saapuisi noin kuukautta myöhemmin sellaiseen kohtaan avaruudessa, missä rakettimoottoria käyttämällä se voisi vääntäytyä L2:n ympärillä olevalle Lissajousin haloradalle.
Tämä vaatii tietysti aika tarkkaa ratalaskentaa ja suunnistamista niin Ariane-rakettien lennättäjiltä kuin Webbin matkantekoa ohjaavalta lennonjohdolta.
24. tammikuuta klo 21 Suomen aikaa illalla Webbin pienet rakettimottorit heräsivät henkiin ja toimivat lähes viiden minuutin ajan (297 sekuntia). Jarruttamisen sijaan moottoreilla lisättiin hieman Webbin nopeutta, noin 1,6 metriä sekunnissa, jolloin se asettui nätisti halutulle radalle.
Koska laukaisu tapahtui niin tarkasti, ettei matkalle L2:n luo tarvittu suuria ratakorjauksia, ja koska saapuminen perillekin sujui erittäin hyvin, on teleskoopilla nyt polttoainetta noin 20 vuoden toimintaa varten. Tästä eteenpäin sitä tarvitaan niihin pieniin ratamuutoksiin, joiden avulla Webb pysyttelee radallaan, ja lisäksi satunnaisesti suurempi asennonkorjauksiin.
Webbin tekeminen, laukaisu ja sen käyttäminen avaruudessa ovat oman juttunsa väärti, mutta tässä yhteydessä tärkeintä on vain se, että kaikki on mennyt paljon paremmin kuin uskallettiin toivoa. Teleskoopin tekeminen oli hidasta ja täynnä hankaluuksia, kun tekniikan rajoja puskettiin monella eri kulmalla, mutta kaikki testaaminen ja erilaisiin vikatilanteisiin varautuminen tuotti selvästi hedelmää.
Raketin nokkaan tiukaksi paketiksi kääritty teleskooppi saatiin avattua suunnitellusti ja nyt sen suuren pääpeilin muodotavia pienempiä kuusikulmaisia peilejä ollaan suuntaamassa. Peilin muotoa voidaan siis muuttaa ja säätää vielä avaruudessa, ja näin tullaan tekemään koko teleskoopin toiminnan ajan. Nyt aluksi tehtävä ensimmäinen säätö on silti kaikkein tärkein, koska nyt 18 peiliosaa säädetään millimetrin absurdisosan tarkkuudella paikalleen.
Sen jälkeen neljää mittalaitetta aletaan ottaa käyttöön, säätää ja kalibroida, ja lopulta kesällä teleskooppi aloittaa rutiininomaiset havainnot.
Mutta Webbiin ennätän palaamaan vielä moneen kertaan.

Mikä on webb: radan halkaisia L2pisteen ympäri ja miten se saadaan siihen pyörimään ja kuvasta päätellen vielä 90¤ kulmaan maa/aurinko ratatasoon nähden.