Ennustaako 300-vuotias laki eksoplaneettojen ratoja?
Optisten apuvälineiden avustaman tähtitieteen ottaessa vielä ensiaskeleitaan, 1700-luvun alkupuoliskolla tunnettiin 17 Aurinkokunnan planeettaa. Tuolloin kaikkia suurempia Aurinkokunnan kappaleita kutsuttiin planeetoiksi, mikä olisi lähinnä linjassa geofysikaalisen planeetan määritelmän kanssa. Sen mukaan planeettoja tunnetaan nykyään ainakin 36, kun kutsumme suurimpia kuita sekundäärisiksi planeetoiksi. Oli kuitenkin jo selvää, ettemme tunteneet jokaista järjestelmämme planeettaa ja tutkijat ymmärsivät, että Aurinkokunnassa saattoi piillä vielä monia tuntemattomia kappaleita. Tähtitieteilijät olivatkin huomaavinaan systematiikkaa planeettojen radoissa. Aivan kuin radat noudattaisivat jonkinlaista matemaattista lainalaisuutta ja laskentakaavaa, jonka perusteella planeettojen rataetäisyydet olisi helppoa muistaa. Jokin mekanismi oli saanut planeetat järjestymään kiertoradoille ihmisen selvitettävissä olevan säännön mukaisesti. Mutta mikä sellainen sääntö voisi olla?
Vuosisadan loppupuoliskolla Johann Daniel Titius ehdotti lainalaisuutta, jossa hän jakoi Saturnuksen ja Auringon välisen etäisyyden sataan yhtä pitkään pituusmittaan. Silloin Merkurius olisi 4 mitan etäisyydellä, Venus 4+3 mitan etäisyydellä Auringosta ja Maa 4+6 mitan etäisyydellä. Edelleen, Mars olisi 4+12 mitan päässä, Jupiter 4+48 mitan ja Saturnus itse 4+96 mitan päässä. Numerot on tarkoituksella kirjoitettu summiksi, joissa jokaisessa on asetettu Merkuriuksen etäisyys, 4 mittaa erikseen. Silloin jokaisen muun planeetan etäisyys lasketaan lisäämällä Merkuriuksen etäisyyteen luku 3 kerrottuna luvulla 2 niin monta kertaa kuin planeetan järjestysnumero edellyttää, jos vain Venukselle annetaan järjestysnumeroksi 0. Tässä hämmentävässä laskukaavassa on tavallaan kyse numerologiasta, jossa etsitään planeettojen rataetäisyyksiin sopiva numeroleikki, mutta koska kaava on hämmästyttävän tarkka ja planeettojen todelliset etäisyydet poikkeavat siitä korkeintaan vain muutamia prosentteja, se sai jonkin verran huomiota aikakauden astronomien keskuudessa. Niin Titius kuin hiukan myöhemmin Johann Elert Bode pitivät ilmeisenä, että vaikka etäisyydellä 4+24 ei kuitenkaan ollut tunnettua planeettaa, kyse oli vain siitä, että sellaista ei oltu vielä onnistuttu havaitsemaan. Lakia ei silti pidetty kovinkaan tärkeänä, vaan sen arveltiin olevan ehkäpä vain sattuman tuotosta.
Tilanne kuitenkin muuttui Uranuksen löydyttyä suunnilleen etäisyydeltä 4+192 vuonna 1781. Vuonna 1801 löydetty Ceres puolestaan sattui lähes täsmälleen Marsin ja Jupiterin väliin jääneeseen aukkokohtaan etäisyydellä 4+24. Tuolloin laki vaikutti sopivan tunnettuihin planeettoihin ja samalla onnistuneen ennustamaan kaksi uutta Aurinkokunnan planeettaa, mikä sai luonnollisesti tähtitieteilijät arvelemaan lain taustalla voivan piillä jotakin fysikaalista tietoa planeettakuntamme rakenteesta. Vaikka se ei enää soveltunut tuleviin löytöihin erityisesti Nep
/tunuksen poiketessa valtavasti ennustetusta, Titius-Boden laki jäi ehkäpä yksinkertaisuutensa ja historian menestyksensä vuoksi elämään astronomien keskuuteen ikään kuin kulttuuriperintönä, eikä sitä unohdettu tulevina vuosisatoina. Siitä tuli osa tähtitieteilijöiden kertomakirjallisuutta, ja laki otetaan toisinaan edelleenkin puheeksi käsiteltäessä yliopiston peruskurssilla tähtitieteen historiaa. Modernina aikakautena lakia ja sen monia variaatioita on myös koetettu soveltaa eksoplaneettajärjestelmiin. Sovelluksia on tuskin koetettu siksi, että olisi uskottu niiden voivan osua oikeaan, vaan ennemminkin siksi, että laskut ovat varsin helppoja.
Titius-Boden laki on oikeastaan vain yksinkertainen eksponentiaalisen kasvun laki, joka sanoo, että planeettojen väliset etäisyydet kasvavat joka askelmalla samalla kertoimella. Historiallisesti, puhuttaessa Aurinkokunnasta, kertoimena on ollu luku 2, vaikka monia muitakin arvoja on ehdotettu. Helpointa on kuitenkin vain määrittää luku planeettakunnasta sovittamalla matemaattisesti eksponentiaalisen kasvun käyrä planeettojen rataetäisyyksiin. Silloin Aurinkokunnan kertoimeksi saadaan noin 1.72 tai hiukan enemmän, riippuen valitusta laskutavasta. Ja koska Aurinkokunnan planeettojen rataetäisyydet sopivat tällaiseen eksponentiaaliseen lakiin niin kovin hyvin, on tavallaan luonnollista kysyä kuinka hyvin sellaiset lait voisivat ennustaa eksoplaneettajärjestelmien rakennetta.
Ennusteita onkin koetettu tuottaa. Kepler -avaruusteleskoopin ensimmäisten havaintojen jälkeen usean planeetan järjestelmiä on tunnettu jo kymmeniä ja yleistetyn Titius-Boden (YTB) lain pohjalta on ennustettu kymmenien planeettojen olemassaolo tunnetuissa järjestelmissä. Ennusteiden ongelmana on kuitenkin se, että vaikka niiden varmentaminen ei tarkemmilla havainnoilla onnistuisikaan, voidaan aina sanoa, että ennusteen mukaisella radalla oleva planeetta on vain liian pieni havaittavaksi vaikkapa ylikulkumenetelmällä. Vaikka ennustettujen planeettojen olemassaolo olisikin joskus mahdollista sulkea pois tarkastelemalla planeettakunnan stabiiliutta ja osoittamalla, että ennustetulla rataetäisyydellä ei ole stabiileja ratoja, sellaiset tilanteet eivät ole kovinkaan yleisiä. Yhden selvän poikkeuksen tarjoaa harvinainen planeettakunta Gliese 876, jossa poikkeuksellisesti kaksi jättiläisplaneettaa kiertää pientä punaista kääpiötähteä hyvin lähellä sekä tähteä että toisiaan. Planeetat ovat resonanssiradoilla, joilla ulompi kiertää tähden kerran aina sisemmän kiertäessä sen kahdesti. Se on ainutlaatuinen planeettakunta, jonka herkkä tasapainotila ja voimakkaat planeettojen väliset vetovoimat suistaisivat YTB ennusteiden mukaiset sisemmät planeetat välittömästi radoiltaan. Voidaan siis olla varmoja, että minkäänlainen YTB laki ei sovellu Gliese 876 tähden kiertolaisiin.
Toiset tähtitieteilijät ovatkin koettaneet varmentaa YTB-lakien tuottamia ennusteita, koska ennusteita tuottaneiden hypoteesien osoittaminen vääriksi on yksi ehkäpä tärkeimpiä tapoja edistää tieteellistä tutkimusta. Käytyään läpi havaintoja kymmenistä järjestelmistä, joille oli tehty ennusteita uusista planeetoista, tutkijat havaitsivat ennusteisiin sopivia uusia planeettoja vain kourallisen. Tulos sai heidät tylysti toteamaan YTB ennusteiden olevan todellisuudessa luotettavuudeltaan kyseenalaisia. Toteamus tarkoittaa käytännössä sitä, että ennustettu planeetta voi joskus olla olemassa, pääasiassa ei, mikä tekee ennusteesta lähinnä arvauksen ja melkoisen perusteettoman pohjan jatkotutkimuksille.
Asiassa on kuitenkin muutakin. Planeetat ovat nimittäin tyypillisesti suunnilleen samassa ratatasossa, joka on vain hyvin harvoin täsmälleen tähden ja havaintolaitteidemme välillä. Planeettojen ratataso voi olla mitä vain, mutta niiden havaitseminen on mahdollista vain siinä harvinaisessa tilanteessa, jossa planeetat kulkevat meidän näkökulmastamme katsottuna tähden editse. Silloin tähteä lähimpänä kiertävät planeetat ovat todennäköisemmin havaittavissa ja kaukaisempien planeettojen ylikulkutodennäköisyys pienenee sitä pienemmäksi mitä kauempana ne ovat. Se taas tarkoittaa, että kaikkia järjestelmien ulko-osiin ennustettuja planeettoja ei voikaan havaita, vaikka ne olisivatkin olemassa. Huomioimalla tämä korjaus, ja vaikka kaikki tähtitieteilijät eivät olekaan samaa mieltä, YTB laeilla saattaa sittenkin olla jonkinlainen tilastollinen ennustevoima.
Kyse on kuitenkin pohjimmiltaan siitä, että planeettakuntien muodostuessa planeettojen radat voivat olla vain niin lähellä toisiaan kuin järjestelmän stabiiliuden puitteissa voivat, mutta eivät yhtään lähempänä. Mikä voidaan tulkita Titius-Boden lakien kaltaisena järjestelmällisyytenä, onkin todellisuudessa vain planeettojen pakkautumista planeettakuntiin sellaisille radoille, joilla ne voivat kiertää tähtiään pitkiä aikoja. Muussa tapauksessa syntyy kaoottista käyttäytymistä ja planeetat joko törmäilevät toisiinsa tai tähteensä tai sinkoutuvat ulos järjestelmästä. Sellaisia planeettakuntia emme tietenkään voi olla havaitsemassa, koska ne ovat jo tuhoutuneet.
Tiedämme eksoplaneettakunnista ainakin sen, että niiden planeetat ovat tosiaan likimain tasaisin välimatkoin tähtiensä kiertoradoilla. Lisäksi planeettakunnissa on tyypillisesti korostetusti samankokoisia planeettoja ja harvemmin suuria kokoeroja. Se vaikuttaa hämmästyttävältä suurten kokoerojen Aurinkokunnasta katsottuna mutta Aurinkokunta ei olekaan täyteen pakattu järjestelmä, koska jättiläisplaneetat ovat vetovoimillaan estäneet tiiviin sisäplaneettakunnan synnyn. Samankaltaiset planeettojen koot johtavat kuitenkin siihen, että planeetat voivat olla suunnilleen tasaisin välimatkoin radoillaan — Gliese 876 järjestelmässä onkin hyvin poikkeuksellisesti Jupiteria massiivisempia planeettoja yhdessä pienten kiviplaneettojen kanssa.
Voidaan siis sanoa, että Titius-Boden laki heijastaa jotakin todellista planeettakunnista, vaikka sitä ei voidakaan pitää hyödyllisenä koetettaessa vaikkapa ennustaa millaisilla radoilla uusia planeettoja voisi todennäköisimmin löytyä. Siksi se pysyy luultavasti tulevaisuudessakin tähtitieteen perinteenä ja esimerkkinä ensimmäisistä yrityksistä ymmärtää miten planeetat valikoivat ratansa. Todellisuus vain on monin verroin yksinkertaisia laskukaavoja mielenkiintoisempi.

Olet oikeassa,
yleinen TB ennusteet ei sovellu Kepler avaruusteleskoopin eksoplaneettajärjestelmiin.
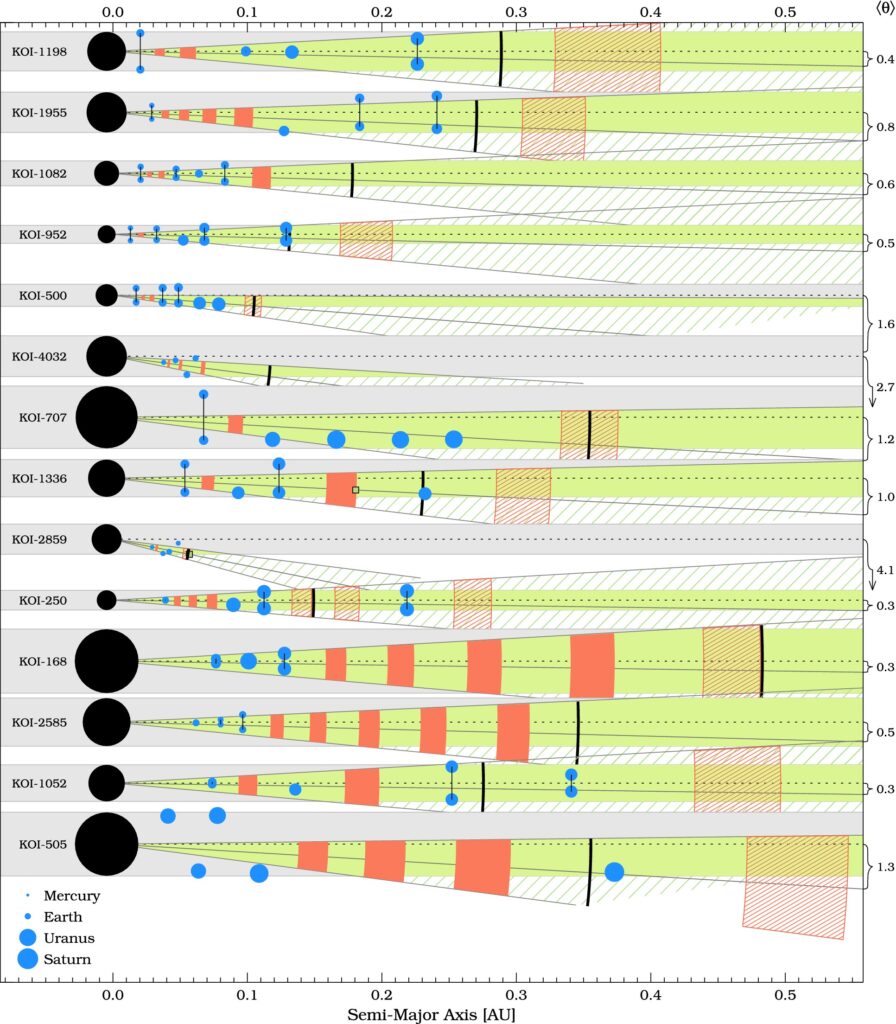
Kuvassa 1. mittakaavassa 14 -järjestelmää (ylhäältä alas laskettuna),
jotka lähellä tähtiään (alle 0,4 AU).
Jokin selkeä jakauma kaikilla kuitenkin näkyy olevan.
Murtolukujen kautta voitte jakaumia etsiä (kokeilemalla eri lukuja).
Löytyneet isoja, massiivisia, joten etäisyydet pienempiin siten suurempia kuin löydetyillä.
Kenties laskemalla löydettyjen massat yhteen voi arvioida suunnilleen etäämpienkin
murtolukujen kertoimia.
Numeroissa: 1, 2, 4, 8, 10, 13 ja 14 osa eksoplaneetoista merkitty rinnakkain viivalla
(kenties kulkevat ns. troijalaisina samaa kiertorataa).
Mikäli osaisin (en nyt osaa) antaa oikeat etäisyyskertoimet, joilla löytäisit uudet
kiertoradat eksoplaneetoille; Voisit nimetä jakaumakertoimet: Tuomina
– suomeksi Tuomi puunimi, mutta Tuomina myös tuontia (uuden tiedon) merkitsevää.
Kaikissa numeroissa näyttäisi olevan eksoplaneetoissa kuitenkin alkuun samaa,
kasvua kuin aurinkokunnassakin planeetoilla: lähellä Aurinkoa pienempää
ja etäämpänä isommat planeetat
(planeettoja pienemmät kuut kytkeytyneet lähellä planeettoihin).
Paljon niitä viivoilla yhdistettyjä eksoplaneettoja pareina kuvassa 1. Kuvassa liki
samoilla parikokoina (siksi kenties päätyneet troijalaisiksi samoille radoilleen).
Eksoplaneetat numerossa 14, lähekkäiset ”troijalaiset” (2 x 2) venyneet
vinomuodostelmaksi (4) toisiinsa nähden – selvä tasapainotila niille muodostunut.