(Kuva: Vesa Kankare, 29.10.06)

Lähes koko sumuinen päivä on mennyt koneen ääressä SWAN-komeetan havaintoja käsitellessä Ursa Minor -juttua varten. Eniten mielenkiintoa keräsi kuitenkin Antti Kuosmasen 29.10. animaation tulosten käsittely.

Sain Ursa Minoria varten muokattua valokäyrän ja pyrstön pituutta kuvaavan käppyrän. Komeetan 24.10. tapahtunut outbursti ja sen jälkeinen himmeneminen saatiin mainiosti havaittua meillä Suomessakin, kuten oheinen käppyrä mainiosti kertoo:

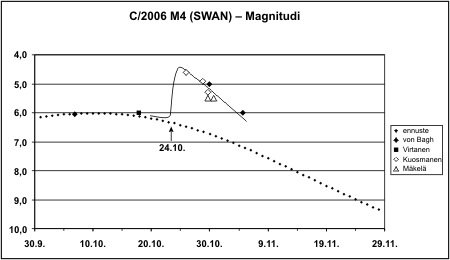
Kuten mainitsin 17.11. viestissäni, komeetta nähtiin maksimisssaan myös paljain silmin.

Hiukan epäselvempi juttu on, vaikuttiko purkaus myös pyrstöön. Jaoston havaintotulokset nimittäin hiukan hajoavat ja ongelmana myöhemmässä vaiheessa on ollut myös se, että pyrstö jatkui monella havaitsijalla kuvakentän ulkopuolelle. Kuitenkin ulkomaisiakin tuloksia vertaamalla, esim. ICQ:n sivuilta voi päätellä, että ennen purkausta pyrstö oli noin puoliasteinen ja venyi sen jälkeen useiden asteiden mittaiseksi:

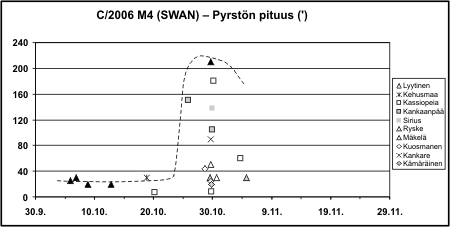
Kasasin myös ehdolle kymmenkunta julkaistavaa kuvaa ja muokkasin niitä samalla harmaasävyisiksi, elleivät olleet jo valmiiksi sellaisia. Pitänee laittaa Kuuren Karille ehdotuksina muutama väri- ja mustavalkokuva vaihtoehtoisesti sijoitettavaksi lehden takakanteen. Samalla voisin liittää mukaan Metsälän Timo-Pekan SWAN-kuvan, jonka hän lähetti pyynnöstäni.

Kaasun vauhtia pyrstössä

Eniten aikaa uhrasin kuitenkin Antti Kuosmasen mainioille animaatioille. Antti otti 28. ja 29.10. yli puolen tunnin sarjat komeetasta, jotka hän ensin kasasi vain yhdeksi otokseksi iltaa kohden, mutta myöhemmin Antti laittoi 15 kuvan sarjat animaatioiksi, joissa näkyy mielenkiintoista liikettä pyrstössä sekä pyrstön sivuilla olevien sivupyrstöjen, ”säteiden”, liikettä.

28.10. 29.10.

Pyrstössä näkyy kaasutihentymien liikettä ja mieleeni juolahti, että noistahan voisi laskea kaasun liikenopeutta pyrstössä. Pyysin Anttia laittamaan minulle 29.10. sarjan ensimmäisen ja viimeisen kuvan, sekä tarkan tiedon kuvien välisestä ajasta.

Ehkä vaikein ja eniten epätarkkuutta aiheuttava seikka oli tunnistaa oikea kaasutihentymä molemmista kuvista. Uskoakseni pääsin tyydyttävään tulokseen veivattuani animaatiota moneen kertaan. Itse asiassa keksin vasta nyt, kuinka sitä voi selaimessa askeltaa kuva kerrallaan ja kelata myös taaksepäin.

Kun olin löytänyt oikean tihentymän, merkkasin sen punaisella värillä kumpaankin kuvaan. Sen jälkeen asetin kuvat päällekkäin PhotoShopissa. Tässä ongelmallisinta oli kohdistaa komeetta samaan kohtaan. Piirsin kuviin koman reunukset kynätyökalulla ja asemoin näiden avulla komeetan mahdollisimman hyvin kohdakkain kummassakin kuvatasossa.

Sen jälkeen vain kaasuryppään liikkeen mittaus mahdollisimman tarkasti ja vastaavan välimatkan etsiminen tähtikentästä tähtipareista ja vastaavan kulman tarkastus TheSky-ohjelmalla.

VAROITUS! Seuraavassa hiukan tylsää matematiikkaa. Kaavoja kammoksuvat hypätkää tekstin loppuun.

1. Kaasutihentymän liikkeeksi sain tyydyttävällä tarkkuudella d = 0′ 57″ = 0,016°
2. Ensimmäinen kuva oli aloitettu 29.10.2006 klo 16.28.29 UT
3. Toinen kuva oli aloitettu 29.10.2006 klo 17.02.07 UT
4. Näistä kuvien väliajaksi t = 33 min 36 s = 2016 s
5. Komeetan etäisyys Maasta efemeridien mukaan oli Δ = 1,009257 AU
6. Josta D = 1,009257 × 149 597 870 km = 150 982 686 km
7. Kaasutihentymän siirtymä k = D tan d = 150 982 686 km × tan 0,016° =
41 723 km
8. Kaasun nopeus v = k / t = 41 723 km / 2016 s =
20,7 km/s

Huomattakoon, että tämä on vain alaraja nopeudelle, koska pyrstö ei ole kohtisuorassa näkösädettämme vastaan. Voimme olettaa, että pyrstö sojottaa suunnilleen poispäin Auringosta. Näin ollen komeetan ns. vaihekulmasta saamme tiedon, miten paljon pyrstö poikkeaa kohtisuorasta.

1. Vaihekulma (efemerideistä) α = 59,88°
2. Kulma näkösäteen kohtisuoraa vastaan β = 90° – α = 30,12°
3. Todellinen kaasun nopeus on noin V = v / cos β = 20,7 / cos 30,12° =
23,9 km/s

Eiköhän siinä ollut laskentoa tälle päivälle ihan tarpeeksi.

Luku saattaa kuullostaa ensi alkuun suurelta, mutta yritin metsästää verkosta vastaavia arvoja. Niitä löytyi niukalti, mutta jossain mainittiin jopa 70 km/s-nopeuksia. Ja muistettakoon, että komeetankin pyrstö kiihdyttävän aurinkotuulen nopeus on satoja kilometrejä sekunnissa.